یادگیری ترکیبی Boosting

Boosting یکی از روش‌های یادگیری ترکیبی است که با هدف کاهش بایاس (Bias) و بهبود دقت مدل‌های یادگیری ماشین طراحی شده است. این روش در سال ۱۹۹۰ توسط رابرت شاپایر (Robert Schapire) و یوآو فروند (Yoav Freund) معرفی شد و بعدها با الگوریتم‌هایی مانند AdaBoost و Gradient Boosting محبوبیت زیادی پیدا کرد. برخلاف Bagging که روی کاهش واریانس تمرکز دارد، بوستینگ با ترکیب مدل‌های پایه (معمولاً مدل‌های ضعیف مانند درخت‌های تصمیم کم‌عمق) به صورت ترتیبی عمل می‌کند تا خطاها را به طور سیستماتیک کاهش دهد.

AdaBoost (Adaptive Boosting) و Gradient Boosting (مانند XGBoost، LightGBM و CatBoost) از معروف‌ترین الگوریتم‌های بوستینگ هستند. این روش برای مسائل پیچیده و داده‌هایی که مدل‌های پایه ساده عملکرد ضعیفی دارند، بسیار مؤثر است. مزیت اصلی بوستینگ، توانایی آن در بهبود دقت مدل با تمرکز بر نمونه‌های دشوار است، اما ممکن است به بیش‌برازش (Overfitting) حساس باشد.

نحوه آموزش و تست داده‌ها

آموزش (Training):

۱. وزن‌دهی اولیه به داده‌ها: در بوستینگ، هر نمونه داده در ابتدا وزن یکسانی دارد (در AdaBoost). در روش‌های دیگر مانند Gradient Boosting، از خطاها یا گرادیان‌های تابع زیان استفاده می‌شود.
۲. آموزش ترتیبی مدل‌های پایه:

• یک مدل پایه (مانند درخت تصمیم کم‌عمق) روی داده‌های آموزشی، آموزش داده می‌شود.
• خطاهای مدل فعلی محاسبه می‌شود (مثلاً نمونه‌هایی که به اشتباه پیش‌بینی شده‌اند).
• وزن نمونه‌های اشتباه افزایش می‌یابد (در AdaBoost) یا مدل بعدی روی گرادیان‌های خطای مدل قبلی تمرکز می‌کند (در Gradient Boosting).
• این فرآیند برای تعداد مشخصی مدل (مثلاً ۱۰۰ یا بیشتر) تکرار می‌شود.
  ۳. ترکیب مدل‌ها: مدل‌های پایه به صورت وزنی (بر اساس عملکردشان) ترکیب می‌شوند. در AdaBoost، مدل‌های قوی‌تر وزن بیشتری در نتیجه نهایی دارند، و در Gradient Boosting، پیش‌بینی‌ها به صورت جمع تراکمی محاسبه می‌شوند.
  ۴. تمرکز بر خطاها: برخلاف Bagging که مدل‌ها مستقل هستند، در boosting هر مدل جدید به خطاهای مدل‌های قبلی توجه می‌کند.

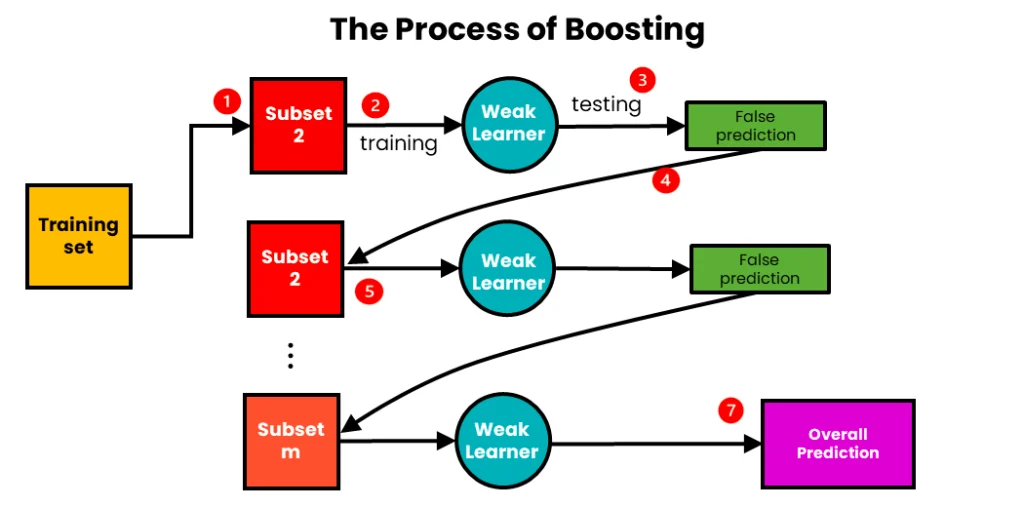
تست (Testing) یا پیش‌بینی:

۱. برای یک داده جدید (از مجموعه تست یا داده‌های واقعی)، پیش‌بینی هر مدل پایه محاسبه می‌شود.
۲. ترکیب پیش‌بینی‌ها:

• در مسائل طبقه‌بندی (Classification): از ترکیب وزنی پیش‌بینی‌ها (مانند رأی‌گیری وزنی در AdaBoost) استفاده می‌شود.
• در مسائل رگرسیون (Regression): پیش‌بینی‌ها به صورت جمع وزنی یا تراکمی محاسبه می‌شوند.
  ۳. این فرآیند باعث می‌شود مدل نهایی روی نمونه‌های دشوار یا پیچیده عملکرد بهتری داشته باشد.

مزایا

• کاهش بایاس: بوستینگ به طور خاص برای کاهش بایاس مدل‌های ضعیف طراحی شده است و می‌تواند دقت را به طور قابل‌توجهی بهبود دهد.
• دقت بالا: در بسیاری از مسائل پیچیده (مانند داده‌های واقعی با روابط غیرخطی)، بوستینگ عملکرد بهتری نسبت به Bagging یا مدل‌های منفرد دارد.
• تمرکز بر نمونه‌های دشوار: با وزن‌دهی به نمونه‌های اشتباه، بوستینگ به بهبود پیش‌بینی در موارد پیچیده کمک می‌کند.
• انعطاف‌پذیری: می‌تواند با انواع مدل‌های پایه و توابع زیان مختلف کار کند (مانند Gradient Boosting با توابع زیان دلخواه).
• کارایی در مسائل نامتوازن: به دلیل تمرکز بر نمونه‌های دشوار، برای داده‌های نامتوازن مناسب است.

معایب

• حساسیت به بیش‌برازش: اگر تعداد مدل‌ها زیاد باشد یا داده‌ها نویزی باشند، بوستینگ ممکن است بیش از حد به داده‌های آموزشی وابسته شود.
• هزینه محاسباتی بالا: آموزش ترتیبی مدل‌ها زمان‌بر است و برخلاف Bagging، امکان موازی‌سازی کامل وجود ندارد.
• پیچیدگی تنظیم پارامترها: بوستینگ معمولاً نیاز به تنظیم دقیق پارامترها (مانند نرخ یادگیری یا عمق درخت‌ها) دارد.
• عدم تفسیرپذیری: مدل نهایی بسیار پیچیده است و تفسیر آن دشوارتر از یک مدل پایه ساده است.
• حساسیت به نویز: در داده‌های بسیار نویزی، تمرکز بیش از حد روی نمونه‌های اشتباه ممکن است عملکرد را کاهش دهد.

داده‌های مناسب برای روش Boosting

روش بوستینگ به‌طور کلی برای مجموعه داده‌هایی با ویژگی‌های زیر مناسب است:

• داده‌های پیچیده با روابط غیرخطی: بوستینگ در داده‌هایی که الگوهای پیچیده‌ای دارند (مانند داده‌های زیستی، مالی یا تصویر) بسیار مؤثر است.
• داده‌های نامتوازن: با تمرکز بر نمونه‌های دشوار، بوستینگ برای مسائل نامتوازن (مانند تشخیص تقلب یا بیماری) مناسب است.
• داده‌های با حجم متوسط تا بزرگ: بوستینگ در مجموعه‌های داده بزرگ‌تر که امکان یادگیری تدریجی خطاها را فراهم می‌کنند، عملکرد بهتری دارد.
• داده‌های با بایاس بالا: اگر مدل پایه (مانند درخت‌های کم‌عمق) به تنهایی عملکرد ضعیفی داشته باشد، بوستینگ می‌تواند بایاس را کاهش دهد.
• داده‌های چندبعدی: در داده‌های با ویژگی‌های زیاد (مانند داده‌های ژنومی یا متنی) به‌خوبی عمل می‌کند.

داده‌های نامناسب برای روش Boosting

• داده‌های بسیار نویزی: بوستینگ ممکن است به نویز بیش از حد حساس شود و روی نمونه‌های نویزی بیش‌برازش کند.
• داده‌های خیلی کوچک: در مجموعه‌های داده کوچک (مثلاً کمتر از چند صد نمونه)، بوستینگ ممکن است به دلیل کمبود تنوع داده‌ها عملکرد ضعیفی داشته باشد.
• داده‌های ساده: اگر روابط در داده‌ها خطی یا ساده باشند (مثل داده‌هایی که با رگرسیون خطی به خوبی مدل می‌شوند)، بوستینگ ممکن است پیچیدگی غیرضروری ایجاد کند.
• داده‌هایی که نیاز به تفسیرپذیری دارند: به دلیل پیچیدگی مدل نهایی، بوستینگ برای کاربردهایی که نیاز به تفسیر آسان دارند مناسب نیست.

معمولاً Boosting در مقایسه با Bagging دقت بالاتری دارد اما حساس‌تر به نویز و overfitting است.

مثال MATLAB یا Python

در زیر یک مثال برای طبقه‌بندی مجموعه داده Iris با استفاده از روش Boosting (به طور خاص AdaBoost) ارائه شده است. در این مثال کد پاییتون، داده‌های گل زنبق (Iris) بارگذاری شده و تنها دو ویژگی اول (طول و عرض کاسبرگ) برای ساده‌سازی تحلیل انتخاب می‌شوند. خروجی شامل سه کلاس گل است. سپس با استفاده از الگوریتم AdaBoost (10 درخت تصمیم) که درخت تصمیم کم‌عمق (max_depth=1) به عنوان مدل پایه در نظر گرفته شده است، مدل آموزش داده می‌شود. در پایان، نواحی تصمیم‌گیری مدل رسم شده و عملکرد طبقه‌بندی به‌صورت بصری نمایش داده می‌شود.

مثال در Python (با استفاده از کتابخانه scikit-learn):

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# بارگذاری داده‌های Iris
iris = load_iris()
X = iris.data[:, :2]  # فقط دو ویژگی اول (طول و عرض کاسبرگ)
y = iris.target

# تقسیم داده‌ها به آموزش و تست
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# ایجاد مدل AdaBoost با درخت تصمیم به عنوان مدل پایه
base_estimator = DecisionTreeClassifier(max_depth=1)  # درخت کم‌عمق
ada_boost = AdaBoostClassifier(base_estimator=base_estimator, n_estimators=10, random_state=42)

# آموزش مدل
ada_boost.fit(X_train, y_train)

# ارزیابی دقت
accuracy = ada_boost.score(X_test, y_test)
print(f"دقت مدل: {accuracy:.2f}")

# رسم نواحی تصمیم‌گیری
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))

# پیش‌بینی برای نواحی تصمیم‌گیری
Z = ada_boost.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# رسم نواحی تصمیم‌گیری و نقاط داده
plt.figure(figsize=(10, 6))
cmap = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
plt.contourf(xx, yy, Z, cmap=cmap, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap, edgecolors='k', s=100)
plt.xlabel('طول کاسبرگ (cm)')
plt.ylabel('عرض کاسبرگ (cm)')
plt.title('نواحی تصمیم‌گیری مدل AdaBoost (Iris)')
plt.show()

در ادامه، یک کد MATLAB برای طبقه‌بندی مجموعه داده Iris با استفاده از روش Boosting (به طور خاص AdaBoost) ارائه شده است. این کد مشابه مثال Python است، اما با استفاده از توابع MATLAB پیاده‌سازی شده است. در این مثال، داده‌های گل زنبق (Iris) بارگذاری شده و تنها دو ویژگی اول (طول و عرض کاسبرگ) برای ساده‌سازی تحلیل انتخاب می‌شوند. خروجی شامل سه کلاس گل است. مدل AdaBoost با 10 درخت تصمیم کم‌عمق آموزش داده می‌شود و نواحی تصمیم‌گیری به صورت بصری نمایش داده می‌شود.

% بارگذاری مجموعه داده Iris
load fisheriris;
X = meas(:, 1:2); % فقط دو ویژگی اول (طول و عرض کاسبرگ)
y = species;      % برچسب‌های کلاس

% تبدیل برچسب‌های رشته‌ای به عددی
[~, ~, y_numeric] = unique(y);

% تقسیم داده‌ها به آموزش و تست
rng(42); % برای تکرارپذیری
cv = cvpartition(length(y), 'HoldOut', 0.3); % 30% برای تست
X_train = X(cv.training, :);
y_train = y_numeric(cv.training);
X_test = X(cv.test, :);
y_test = y_numeric(cv.test);

% ایجاد و آموزش مدل AdaBoost
base_model = fitctree(X_train, y_train, 'MaxDepth', 1); % درخت تصمیم کم‌عمق
ada_model = fitcensemble(X_train, y_train, 'Method', 'AdaBoostM2', ...
                         'NumLearningCycles', 10, 'Learners', base_model);

% ارزیابی دقت مدل
y_pred = predict(ada_model, X_test);
accuracy = sum(y_pred == y_test) / length(y_test);
fprintf('دقت مدل: %.2f\n', accuracy);

% رسم نواحی تصمیم‌گیری
x_min = min(X(:,1)) - 1; x_max = max(X(:,1)) + 1;
y_min = min(X(:,2)) - 1; y_max = max(X(:,2)) + 1;
[xx, yy] = meshgrid(x_min:0.01:x_max, y_min:0.01:y_max);
X_grid = [xx(:), yy(:)];

% پیش‌بینی برای نواحی تصمیم‌گیری
Z = predict(ada_model, X_grid);
Z = reshape(Z, size(xx));

% رسم نواحی تصمیم‌گیری و نقاط داده
figure;
contourf(xx, yy, Z, 'LineStyle', 'none');
colormap([1 0.7 0.7; 0.7 1 0.7; 0.7 0.7 1]); % رنگ‌های متمایز
hold on;
gscatter(X(:,1), X(:,2), y, 'rbg', 'o', 5, 'filled'); % نقاط داده
xlabel('طول کاسبرگ (cm)');
ylabel('عرض کاسبرگ (cm)');
title('نواحی تصمیم‌گیری مدل AdaBoost (Iris)');
legend('Location', 'best');
hold off;

پس از بارگزاری داده های iris و تقسمی بندی آن ها به صورت 70 به 30 برای آموزش و تست، تابع fitcensemble با روش AdaBoostM2 (مناسب برای مسائل چندکلاسه) استفاده شده و 10 درخت تصمیم کم‌عمق (MaxDepth=1) به عنوان مدل پایه آموزش داده می‌شوند. نتایج بصری نیز با استفاده از meshgrid کد نویسی شده است.