تبدیل فوریه سیگنال
تبدیل فوریه سیگنال
مقدمه
تبدیل فوریه یکی از ابزارهای اساسی در پردازش سیگنال و تحلیل ریاضی است که امکان تجزیه سیگنالها به مؤلفههای فرکانسی را فراهم میکند. این تبدیل برای تحلیل سیگنالهای پیوسته و گسسته، بهویژه در حوزههای مهندسی برق، مخابرات، پردازش صوت و تصویر، و علوم داده کاربرد گستردهای دارد. در این مقاله، مفهوم تبدیل فوریه، فرمولهای ریاضی آن، و پیادهسازی عملی در متلب بررسی میشود. همچنین، با ارائه مثالهای عملی و کدهای بهبودیافته، تحلیل فرکانسی سیگنالها بهصورت جامع توضیح داده خواهد شد.
تبدیل فوریه چیست؟
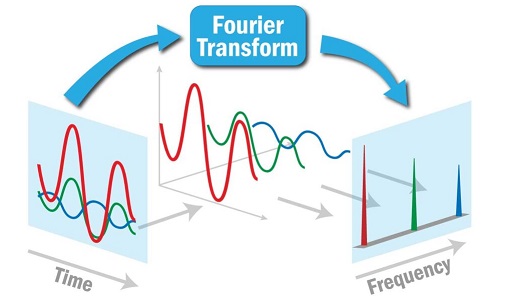
تبدیل فوریه سیگنالهای زمانی (در حوزه زمان) را به حوزه فرکانس منتقل میکند و محتوای فرکانسی آنها را نمایش میدهد. این تبدیل نشان میدهد که یک سیگنال از چه مؤلفههای فرکانسی تشکیل شده و هر فرکانس با چه دامنهای در سیگنال حضور دارد. تبدیل فوریه برای سیگنالهای پیوسته و گسسته به ترتیب بهصورت زیر تعریف میشود:
تبدیل فوریه پیوسته (CFT)
برای یک سیگنال پیوسته x(t) ، تبدیل فوریه بهصورت زیر است:
که در آن:
- X(f) : طیف فرکانسی سیگنال.
- f: فرکانس (برحسب هرتز).
: هسته تبدیل فوریه که شامل مؤلفههای سینوسی و کسینوسی است.
تبدیل فوریه گسسته (DFT)
برای سیگنالهای گسسته x[n] ، تبدیل فوریه گسسته بهصورت زیر تعریف میشود:
که در آن:
- N : تعداد نمونهها.
- k : شاخص فرکانس.
- X(k): طیف فرکانسی در فرکانسهای گسسته.
تبدیل فوریه سریع (FFT) نسخه محاسباتی بهینهشده DFT است که در عمل برای تحلیل سیگنالهای گسسته استفاده میشود.
شرایط استفاده
برای استفاده از تبدیل فوریه، سیگنال باید:
- در بازه موردنظر انتگرالپذیر باشد (برای سیگنالهای پیوسته).
- انرژی محدودی داشته باشد یا بهصورت عملی قابل نمونهبرداری باشد.
کاربردهای تبدیل فوریه
تبدیل فوریه در حوزههای مختلفی کاربرد دارد، از جمله:
- پردازش سیگنال: شناسایی مؤلفههای فرکانسی در سیگنالهای صوتی، رادار، و مخابراتی.
- فشردهسازی داده: کاهش حجم دادهها با حذف فرکانسهای غیرضروری (مانند فشردهسازی MP3).
- فیلتر کردن سیگنال: حذف نویز یا مؤلفههای فرکانسی ناخواسته.
- تحلیل سیستمها: بررسی پاسخ فرکانسی سیستمهای خطی در مهندسی کنترل.
محدودیتها
- سیگنالهای غیرایستا: تبدیل فوریه اطلاعات زمانی تغییرات فرکانسی را نشان نمیدهد. برای سیگنالهای غیرایستا، روشهایی مانند تبدیل فوریه زمان کوتاه (STFT) یا تبدیل ویولت مناسبتر هستند.
- محدودیتهای عددی: در پیادهسازیهای عملی، دقت نمونهبرداری و طول سیگنال بر کیفیت تحلیل تأثیر میگذارد.
- پدیده نشت فرکانسی (Spectral Leakage): اگر سیگنال بهصورت کامل متناوب نباشد، ممکن است پیکهای فرکانسی پخش شوند.
پیادهسازی تبدیل فوریه در متلب
برای تحلیل فرکانسی سیگنالها در متلب، از الگوریتم FFT استفاده میشود. در ادامه، مثالی از یک سیگنال ترکیبی سینوسی ارائه شده و با استفاده از FFT تحلیل میشود.
مثال: سیگنال سینوسی ترکیبی
فرض کنید سیگنالی بهصورت زیر تعریف شود:
این سیگنال شامل سه مؤلفه فرکانسی با فرکانسهای 10، 50، و 100 هرتز است. هدف، محاسبه و نمایش طیف فرکانسی این سیگنال است.
% پارامترهای سیگنال
fs = 1000; % فرکانس نمونهبرداری (Hz)
t = 0:1/fs:1; % بازه زمانی (1 ثانیه)
f = [10, 50, 100]; % فرکانسهای سیگنال (Hz)
A = [2, 1, 0.5]; % دامنههای سیگنال
% تولید سیگنال
signal = A(1)*sin(2*pi*f(1)*t) + A(2)*sin(2*pi*f(2)*t) + A(3)*sin(2*pi*f(3)*t);
% محاسبه تبدیل فوریه
N = length(signal);
Y = fft(signal);
f_axis = (0:N-1)*(fs/N); % محور فرکانس
amplitude = abs(Y)/N; % دامنه نرمالشده
% رسم سیگنال در حوزه زمان
figure;
subplot(2,1,1);
plot(t, signal, 'LineWidth', 1.5);
xlabel('زمان (ثانیه)'); ylabel('دامنه');
title('سیگنال سینوسی ترکیبی در حوزه زمان');
grid on;
% رسم طیف فرکانسی
subplot(2,1,2);
plot(f_axis(1:N/2), amplitude(1:N/2), 'LineWidth', 1.5);
xlabel('فرکانس (Hz)'); ylabel('دامنه');
title('طیف فرکانسی سیگنال');
grid on;
توضیحات کد
- پارامترهای سیگنال: فرکانس نمونهبرداری ( fs = 1000 Hz) و بازه زمانی (1 ثانیه) تعریف شده است.
- تولید سیگنال: سیگنال ترکیبی با سه مؤلفه فرکانسی تولید میشود.
- محاسبه FFT: با استفاده از تابع
FFT، طیف فرکانسی محاسبه میشود. - نمایش نتایج: سیگنال در حوزه زمان و طیف فرکانسی در دو نمودار جداگانه نمایش داده میشود.
تحلیل نتایج
- نمودار حوزهزمان، سیگنال ترکیبی سینوسی را نشان میدهد که ترکیبی از سه فرکانس است.
- نمودار طیف فرکانسی، سه پیک مشخص در فرکانسهای 10، 50، و 100 هرتز را نمایش میدهد که دامنههای آنها به ترتیب 2، 1، و 0.5 است.
نتیجهگیری
تبدیل فوریه ابزاری قدرتمند برای تحلیل فرکانسی سیگنالها است که در پردازش سیگنال کاربردهای گستردهای دارد. برای سیگنالهای ایستا، تبدیل فوریه استاندارد (یا FFT) کافی است، اما برای سیگنالهای غیرایستا، روشهای زمان-فرکانس مانند STFT یا تبدیل ویولت مناسبتر هستند. کدهای ارائهشده در این مقاله میتوانند بهعنوان پایهای برای تحلیل سیگنالهای مختلف در متلب استفاده شوند.
برای مطالعه بیشتر، کتابهایی مانند “Signals and Systems” نوشته اپنهایم و منابع پردازش سیگنال توصیه میشود.














