مقدمه

تبدیل فوریه زمان کوتاه (Short-Time Fourier Transform یا STFT) یکی از ابزارهای کلیدی در پردازش سیگنال است که برای تحلیل سیگنال‌های غیرایستا، که محتوای فرکانسی آن‌ها در طول زمان تغییر می‌کند، استفاده می‌شود. برخلاف تبدیل فوریه استاندارد که تنها اطلاعات فرکانسی را ارائه می‌دهد، STFT اطلاعات فرکانسی را همراه با تغییرات زمانی آن‌ها نمایش می‌دهد. این روش در حوزه‌هایی مانند پردازش صوت، تحلیل گفتار، رادار، و تشخیص عیوب ماشین‌آلات کاربرد گسترده‌ای دارد.

تبدیل فوریه زمان کوتاه (STFT)

تبدیل فوریه زمان کوتاه سیگنال را به بخش‌های کوچک‌تر تقسیم کرده و برای هر بخش، تبدیل فوریه را محاسبه می‌کند. این کار با استفاده از یک پنجره زمانی (مانند پنجره همینگ یا گاوسی) انجام می‌شود که روی سیگنال اعمال شده و امکان تحلیل تغییرات فرکانسی در طول زمان را فراهم می‌کند. نتیجه STFT یک اسپکتروگرام است که توزیع انرژی سیگنال را در حوزه زمان-فرکانس نمایش می‌دهد.

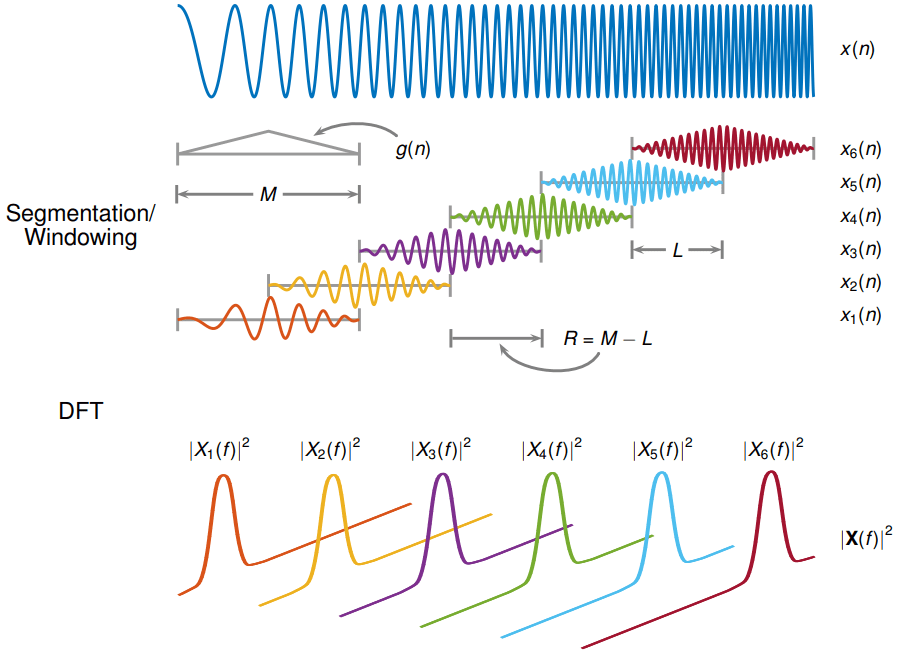
فرمول ریاضی STFT

برای یک سیگنال پیوسته ( x(t) )، تبدیل فوریه زمان کوتاه به‌صورت زیر تعریف می‌شود:
$$
\mathrm{STFT}_x(m,\omega) = \int_{-\infty}^{\infty} x(t)\, w(t – m)\, e^{-j \omega t} \, dt
$$

که در آن:

• x(t): سیگنال ورودی.
• w(t-m): پنجره زمانی که در زمان ( m ) جابجا شده است.
• w : فرکانس زاویه‌ای (رادیان بر ثانیه).
• ( STFTx(t)(m,w: مقدار تبدیل در زمان ( m ) و فرکانس w.

برای سیگنال‌های گسسته ( x[n] )، STFT به‌صورت زیر است:

که در آن:

• w[n-m] : پنجره گسسته جابجا شده.
• N : تعداد نقاط در تبدیل فوریه.
• k : شاخص فرکانس.

شرایط استفاده

برای استفاده از STFT، سیگنال باید:

• قابل نمونه‌برداری باشد (برای سیگنال‌های گسسته).
• پنجره زمانی مناسب انتخاب شود تا تعادل بین وضوح زمانی و فرکانسی حفظ شود.

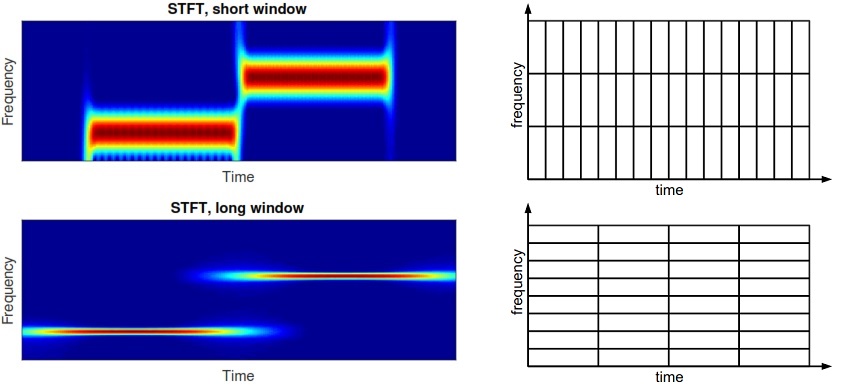
انتخاب پنجره مناسب

تاثیر انتخاب پنجره بر رزولوشن فرکانسی و زمانی به خوبی در عکس زیر نشان داده شده است. هرچه پنجره در حوزه زمان باریک تر رزولوشن فرکانسی بدتر می شود و هر چه سیگنال در حوزه زمانی پخش تر باشد به همان نسبت رزولوشن فرکانسی بهتر خاهد بود و خط های نمایش داده شده در اسپکتروم باریک تر می باشد.

پیاده‌سازی STFT در متلب

برای تحلیل سیگنال‌های غیرایستا در متلب، از تابع spectrogram استفاده می‌شود که STFT را محاسبه کرده و اسپکتروگرام را نمایش می‌دهد. در ادامه، مثالی از یک سیگنال چیرپ (Chirp) ارائه شده و با STFT تحلیل می‌شود.

مثال: سیگنال چیرپ

سیگنال چیرپ یک سیگنال غیرایستا است که فرکانس آن به‌تدریج در طول زمان تغییر می‌کند. فرض کنید سیگنالی با فرکانس اولیه 10 هرتز و فرکانس نهایی 100 هرتز داریم.

% پارامترهای سیگنال
fs = 1000; % فرکانس نمونه‌برداری (Hz)
t = 0:1/fs:2; % بازه زمانی (2 ثانیه)
f0 = 10; % فرکانس اولیه (Hz)
f1 = 100; % فرکانس نهایی (Hz)

% تولید سیگنال چیرپ
signal = chirp(t, f0, t(end), f1, 'linear');

% محاسبه STFT
window = hamming(128); % پنجره همینگ
noverlap = 120; % تعداد نمونه‌های هم‌پوشانی
nfft = 256; % تعداد نقاط FFT
[s, f, t_stft] = spectrogram(signal, window, noverlap, nfft, fs);

% رسم سیگنال در حوزه زمان
figure;
subplot(2,1,1);
plot(t, signal, 'LineWidth', 1.5);
xlabel('زمان (ثانیه)'); ylabel('دامنه');
title('سیگنال چیرپ در حوزه زمان');
grid on;

% رسم اسپکتروگرام
subplot(2,1,2);
surf(t_stft, f, 10*log10(abs(s)), 'EdgeColor', 'none');
axis tight; view(0, 90);
xlabel('زمان (ثانیه)'); ylabel('فرکانس (Hz)');
title('اسپکتروگرام سیگنال چیرپ');
colorbar;

پارامترهای سیگنال: فرکانس نمونه‌برداری fs = 1000 Hz، بازه زمانی (2 ثانیه)، و فرکانس‌های اولیه و نهایی تعریف شده‌اند.

1. تولید سیگنال چیرپ: سیگنال چیرپ با فرکانس متغیر از 10 هرتز به 100 هرتز تولید می‌شود.
2. محاسبه STFT: تابع spectrogram با استفاده از پنجره همینگ، هم‌پوشانی، و تعداد نقاط FFT، تبدیل فوریه زمان کوتاه را محاسبه می‌کند.
3. نمایش نتایج: سیگنال در حوزه زمان و اسپکتروگرام در حوزه زمان-فرکانس نمایش داده می‌شود.

تحلیل نتایج

• نمودار حوزه زمان: سیگنال چیرپ را نشان می‌دهد که دامنه آن ثابت است، اما فرکانس از 10 هرتز به 100 هرتز افزایش می‌یابد.
• اسپکتروگرام: تغییرات فرکانسی در طول زمان را به‌وضوح نمایش می‌دهد، برخلاف تبدیل فوریه استاندارد که تنها حضور فرکانس‌ها را نشان می‌دهد.

کاربردهای STFT

تبدیل فوریه زمان کوتاه در حوزه‌های مختلفی کاربرد دارد، از جمله:

• پردازش گفتار و صوت: تحلیل تغییرات فرکانسی در سیگنال‌های گفتاری یا موسیقی.
• تحلیل رادار و سونار: شناسایی سیگنال‌های غیرایستا در سیستم‌های راداری.
• تشخیص عیوب ماشین‌آلات: بررسی تغییرات فرکانسی در ارتعاشات برای شناسایی خرابی‌ها.
• پردازش تصویر: تحلیل ویژگی‌های فرکانسی در تصاویر متغیر زمانی.

محدودیت‌ها

• تعادل زمان-فرکانس: انتخاب اندازه پنجره تأثیر زیادی بر وضوح زمانی و فرکانسی دارد. پنجره‌های کوچک‌تر وضوح زمانی بهتری دارند، اما وضوح فرکانسی کمتری ارائه می‌دهند و بالعکس.
• محدودیت‌های عددی: دقت نمونه‌برداری، اندازه پنجره، و هم‌پوشانی بر کیفیت اسپکتروگرام تأثیر می‌گذارند.
• پیچیدگی محاسباتی: STFT نسبت به تبدیل فوریه استاندارد محاسبات بیشتری نیاز دارد.

نتیجه‌گیری

تبدیل فوریه زمان کوتاه (STFT) ابزاری قدرتمند برای تحلیل سیگنال‌های غیرایستا است که امکان بررسی تغییرات فرکانسی در طول زمان را فراهم می‌کند. این روش به‌ویژه برای کاربردهایی که نیاز به تحلیل زمان-فرکانس دارند، مانند پردازش گفتار و رادار، مناسب است. کدهای ارائه‌شده در این مقاله می‌توانند به‌عنوان پایه‌ای برای تحلیل سیگنال‌های غیرایستا در متلب استفاده شوند.